Présentation
Auteur(s)
-
Jacques POIRIER : Ingénieur de l’École Centrale de Paris, Docteur-Ingénieur - Conseiller du Directeur des Réacteurs Nucléaires au Commissariat à l’Énergie Atomique - Chargé de mission auprès des Secrétaires Perpétuels de l’Académie des Sciences - Professeur associé au Conservatoire National des Arts et Métiers
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleINTRODUCTION
L’ingénieur doit très souvent répondre à une question d’importance pratique considérable, qui est : « est-ce que tel ou tel facteur influence le résultat de mesure ? » Plus précisément, de telles questions peuvent être : « Est‐ce que telle impureté affecte les caractéristiques mécaniques de tel matériau ?» ou bien : « Est-ce que tous les opérateurs conduisant tel gros appareil en travail posté aboutissent effectivement au même résultat, à la même qualité ? » ou bien : « Est‐ce que tel paramètre, qu’on a de bonnes raisons physiques d’estimer important, influence réellement les résultats de mesure ? »
L’outil privilégié pour effectuer ce genre d’étude est l’analyse de la variance.
Nous examinerons successivement l’analyse de la variance à simple entrée (§ 2 et 3), où l’on cherche à déterminer l’influence d’un seul facteur, puis l’analyse de la variance à double entrée (§ 4 et 5 : deux facteurs, ayant éventuellement une interaction entre eux) et le cas particulier de l’analyse de la variance emboîtée 6.
L’influence d’un facteur
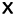sur un résultat de mesure
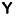ayant été mise en évidence, il est souvent utile de chercher à préciser cette liaison entre deux variables : la méthode de régression 7 a pour objet la recherche d’une fonction représentant cette liaison.
Cet article fait suite aux articles Observation statistique Observation statistique, Estimateurs et tests d’hypothèses Estimateur et tests d’hypothèses, auxquels il est fait référence dans le cours du texte ; les tables numériques se trouvent dans l’article Tables statistiques Tables statistiques.
L'expertise technique et scientifique de référence
DOI (Digital Object Identifier)
CET ARTICLE SE TROUVE ÉGALEMENT DANS :
Accueil > Ressources documentaires > Mesures - Analyses > Instrumentation et méthodes de mesure > Méthodes de mesure > Analyse de la variance et de la régression. Plans d’expérience > Modèles mathématiques et espérance mathématique des quotients : remarques
Cet article fait partie de l’offre
Métier : responsable qualité
(252 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Carré latin et analyse de la variance emboîtée5. Modèles mathématiques et espérance mathématique des quotients : remarques
Une fois qu’a été déterminé au seuil α si tel ou tel effet est significatif, il est possible de construire un (ou des) modèle(s) mathématique(s) permettant d’affiner l’analyse et d’en tirer les conclusions ultimes.
5.1 Cas où le choix des niveaux des facteurs contrôlés est systématique
On peut poser :
Dans cette expression :
-
ξab β est la fluctuation – gaussienne – due aux facteurs non contrôlés ;
-
λ0 est une constante ;
-
![]()
(respectivement
![]()
) est une correction systématique pour tous les résultats du même niveau du facteur A (respectivement B) ; -
![]()
est une correction systématique complémentaire pour tous les couples de niveaux des facteurs A et B (donc pour toutes les mesures correspondant à une case du tableau 6 d’analyse de la variance).
(respectivement
) est une correction systématique pour tous les résultats du même niveau du facteur A (respectivement B) ;
est une correction systématique complémentaire pour tous les couples de niveaux des facteurs A et B (donc pour toutes les mesures correspondant à une case du tableau De façon intuitive,
rendront compte, niveau par niveau, des effets principaux et, de façon analogue,
rendra compte de l’interaction. On peut choisir λ 0 de telle sorte que, simultanément :
L'expertise technique et scientifique de référence
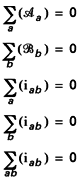
Cet article fait partie de l’offre
Métier : responsable qualité
(252 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Modèles mathématiques et espérance mathématique des quotients : remarques
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Métier : responsable qualité
(252 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
