Bibliographie & annexes
Quiz & test
Présentation
En anglais
RÉSUMÉ
Cet article aborde la notion de systèmes linéaires invariants et détaille les différents types de représentations qui leur sont rattachés : la représentation fréquentielle classique, puis la représentation d’état. Grâce au fort développement des moyens de calcul, la représentation d’état est maintenant la plus utilisée, au niveau de la simulation mais plus encore au niveau de la commande. Le cas plus général des systèmes linéaires incertains est ensuite abordé et une représentation associée, dite LFT, généralisant les représentations précédentes est présentée. Cet article s’achève par des aspects logiciels illustrant les différentes représentations et propose des moyens simples de les manipuler.
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleABSTRACT
This article discusses the notion of invariant linear systems and details their different types of representation from standard frequency-domain transfer functions to state-space representations. Thanks to the strong development of computational capacities, state-space representations are now widely used, not only for simulation purpose but also for control design. The more general case of uncertain linear systems is then discussed and an associated LFT (Linear Fractional transformation) representation, generalizing the previous ones is presented. This article concludes with software aspects illustrating the different representations and proposes simple ways to manipulate them.
Auteur(s)
-
Jean-Marc BIANNIC : Directeur de recherche à l’ONERA – Professeur à ISAE / SUPAÉRO - ONERA-DTIS, Toulouse, France
INTRODUCTION
Le texte qui suit constitue une mise à jour de l’article [S 7 130] paru en 2006 intitulé « Représentations d’un système linéaire » rédigé par André FOSSARD et Jean-Marc BIANNIC à partir de la version initiale du dossier de Marc CLIQUE et Jean-Charles GILLE intitulé « Représentation d’un système ». Tous les éléments de la version de 2006 sont conservés dans cet article qui comporte en outre une nouvelle section majeure dédiée aux systèmes linéaires incertains. L’introduction d’incertitudes dans la modélisation des systèmes linéaires est essentielle dans la mesure où très souvent, de nombreux paramètres sont mal connus. Plutôt que de manipuler un grand nombre de systèmes associés à différentes valeurs possibles de ces paramètres, l’objectif est de proposer une formulation plus générale sous la forme d’un système unique dans laquelle toutes les incertitudes sont regroupées au sein d’un opérateur incertain dont la structure est diagonale par blocs. Ce type de formulation, dit LFT (« Linear Fractional Transformation ») est particulièrement bien adapté aux techniques de synthèse de lois de commande robustes aux incertitudes et aux techniques d’analyse de la robustesse, tout en facilitant également la simulation. La section suivante, dédiée aux aspects logiciels sous MATLAB, est étoffée pour illustrer comment modéliser très simplement un système linéaire incertain grâce à la définition d’un « objet » dédié. Enfin, la bibliographie est mise à jour avec plusieurs références spécifiques à cette modélisation LFT.
L'expertise technique et scientifique de référence
KEYWORDS
Linear systems | Transfer functions | State-space representation | LFT
VERSIONS
- Version archivée 1 de déc. 2006 par André FOSSARD, Jean-Marc BIANNIC
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Aspects logiciels
En anglais
7. Extension aux systèmes incertains : modélisation LFT
Dans ce qui précède, les matrices A, B, C, D de la représentation d’état ont toutes été supposées bien connues. C’est cependant rarement le cas en pratique dans la mesure où ces matrices dépendent généralement, pour diverses raisons de paramètres incertains. On est alors amené à manipuler un grand nombre (voire une infinité) de représentations associées aux diverses combinaisons paramétriques possibles. Pour éviter cette lourdeur, une représentation spécifique est proposée ici. Elle repose sur la notion de transformations linéaires fractionnelles (Linear Fractional Transformations) et on parle donc de modèle ou de représentation LFT. Une introduction simple est proposée dans cette section à partir d’une illustration graphique sur un modèle du second ordre.
7.1 Illustration graphique sur un modèle du second ordre
On considère ici un modèle du second ordre, de gain statique unitaire, de pulsation ω et d’amortissement ξ dont une représentation d’état classique est donnée par :
On suppose maintenant que la pulsation est mal connue et on introduit une incertitude multiplicative δ sur ce paramètre qui s’écrit alors :
où ω0 désigne la pulsation nominale. Il en résulte une représentation d’état dont les matrices A et B dépendent toutes deux de l’incertitude paramétrique avec ici une dépendance polynomiale de par la présence de δ et δ2 . L’objectif est d’obtenir une représentation simplifiée au sein de laquelle le paramètre δ sera isolé et apparaîtra simplement (sans élévation au carré) au prix d’une éventuelle répétition. Pour cela, le système est préalablement réécrit sous la forme :
...
L'expertise technique et scientifique de référence
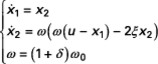
TEST DE VALIDATION ET CERTIFICATION CerT.I. :
Cet article vous permet de préparer une certification CerT.I.
Le test de validation des connaissances pour obtenir cette certification de Techniques de l’Ingénieur est disponible dans le module CerT.I.
de Techniques de l’Ingénieur ! Acheter le module
Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Extension aux systèmes incertains : modélisation LFT
BIBLIOGRAPHIE
-
(1) - GILLE (J.-CH.), CLIQUE (M.) - Systèmes linéaires. Équations d’état –. - Eyrolles, 2e éd (1990).
-
(2) - GILLE (J.-CH.), CLIQUE (M.) - Calcul matriciel et introduction à l’analyse fonctionnelle pour ingénieurs – - 3 tomes Lidec, Montréal, 6e édition 2000 (1re édition Eyrolles 1979) ISBN 2-7608-6121-X.
-
(3) - FOSSARD (A. J) - Représentation, observation et commande des systèmes linéaires dans l’espace d’état – Systèmes mono-entrée, mono-sortie. - ENSAE Toulouse France, ISBN 2.84088.023-7 (1995).
-
(4) - DORF (R.C.), BISHOP (R.H.) - Modern Control System – - Prentice Hall, 10th edition (2004).
-
(5) - MINZU (V.), LANG (B.) - Commande des systèmes linéaires continus – Cours avec applications utilisant MATLAB – - Ellipses (2001).
-
...
DANS NOS BASES DOCUMENTAIRES
-
Connaissance d’un système.
ANNEXES
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
QUIZ ET TEST DE VALIDATION PRÉSENTS DANS CET ARTICLE
1/ Quiz d'entraînement
Entraînez vous autant que vous le voulez avec les quiz d'entraînement.
2/ Test de validation
Lorsque vous êtes prêt, vous passez le test de validation. Vous avez deux passages possibles dans un laps de temps de 30 jours.
Entre les deux essais, vous pouvez consulter l’article et réutiliser les quiz d'entraînement pour progresser. L’attestation vous est délivrée pour un score minimum de 70 %.
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
