Présentation
En anglais
Auteur(s)
-
Claude ROUXEL : Enseignant au Conservatoire National des Arts et Métiers
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleINTRODUCTION
Les nombres complexes sont très utilisés en électricité. L’idée de base pour construire cet ensemble de nombres est d’adjoindre à l’ensemble
des réels, un nouveau nombre, noté
, dont le carré vaut (–1).
Ce nouvel ensemble de nombres est conçu de façon à :
-
conserver les règles opératoires sur les réels (associativité, commutativité, distributivité...) ;
-
tenir compte de la nouvelle règle :
= –1.
On démontre alors que les nombres complexes peuvent s’écrire, de façon unique, sous la forme dite cartésienne :
où a et b sont des réels.
L'expertise technique et scientifique de référence
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Conversion de l'énergie électrique
(269 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Forme cartésienne des nombres complexes
En anglais
5. Transformation cissoïdale
Dans cette partie, nous adoptons la convention qui consiste à souligner les variables complexes.
5.1 Définition
Considérons un signal sinusoïdal de pulsation ω appliqué à un système linéaire :
En développant le sinus, on peut aussi l’écrire :
avec :
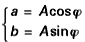
égalités équivalentes à :
En régime permanent, c’est-à-dire lorsque les grandeurs d’entrée et de sortie d’un système linéaire sont stables dans le temps, on veut pouvoir raisonner sur les paramètres (ω, A, ϕ ) de la fonction sans faire intervenir le temps.
On est ainsi amené à définir la transformation cissoïdale en associant à f le nombre complexe :
Note : le mot « cis » vient de la contraction de « cosinus i sinus ».
On a alors avantage à considérer la fonction f (t ) = Asin(ωt + ϕ ) comme la partie imaginaire de la fonction complexe :
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Conversion de l'énergie électrique
(269 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Transformation cissoïdale
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Conversion de l'énergie électrique
(269 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
