Présentation
RÉSUMÉ
La méthode des éléments finis est utilisée pour résoudre les équations de Navier-Stokes. Cette méthode est très bien adaptée à l’approximation des équations régissant le comportement de fluides et permet aussi de fournir une approximation des domaines de définition des équations à résoudre, en particulier pour la prise en compte de frontières courbes. La résolution de ces équations avec diverses conditions aux limites et avec divers éléments finis admissibles est présentée. Des résultats de majoration d’erreur sont indiqués. Plusieurs méthodes diverses de résolution des systèmes discrétisés sont présentées. Enfin quelques applications ainsi que des codes d’éléments finis comparés à ceux en volumes finis sont indiqués et permettent de dégager des critères de choix de codes industriels.
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleAuteur(s)
-
Pierre SPITERI : Professeur émérite - Université de Toulouse, INP – ENSEEIHT – IRIT, Toulouse, France
INTRODUCTION
Dans l’article [AF 1 404] nous avons présenté les concepts méthodologiques conduisant à la modélisation par l’équation de Navier-Stokes des phénomènes d’écoulements de fluides incompressibles ou compressibles, laminaires ou turbulents. Pour résoudre numériquement ces équations par différences finies nous avons considéré, d’une part, la formulation courant-vorticité qui conduit à la résolution d’équations de Poisson couplées à des équations de convection-diffusion et, d’autre part, la formulation vitesse-pression. Cependant l’approximation de problèmes aux limites par différences finies si elle est intéressante lorsque le domaine Ω est de forme rectangulaire présente par contre des difficultés de mise en œuvre lorsque Ω est de forme quelconque. C’est pourquoi dans l’industrie on utilise de préférence la méthode des éléments finis qui permet à la fois d’obtenir une approximation des opérateurs aux dérivées partielles ainsi que du domaine Ω. On a vu également dans l’article [AF 1 406] la résolution des équations de Navier-Stokes par la méthode des volumes finis.
Pour des raisons de simplicité d’exposition on se limitera dans cet article au cas de problèmes bidimensionnels stationnaires ; habituellement on discrétise les dérivées par rapport au temps par différences finies pour aboutir soit à des schémas en temps de type explicite soit à des schémas en temps de type implicite, puis on utilise la méthode des éléments finis pour discrétiser spatialement le problème semi-discrétisé en temps. Que cela soit l’un ou l’autre schéma en temps, le point crucial est donc constitué par l’approximation spatiale des opérateurs. On abordera aussi la discrétisation temporelle par élément finis.
Compte tenu de la complexité de l’approximation du problème cible par éléments finis, nous nous bornerons dans un premier temps à l’approximation par éléments finis du problème linéaire de Stokes, correspondant aux équations de Navier-Stokes sans le terme non linéaire de convection. De plus toujours pour simplifier l’exposé nous supposerons que les conditions aux limites sont de type Dirichlet homogènes, c’est-à-dire que
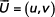 est nulle sur la frontière ∂Ω du domaine Ω.
est nulle sur la frontière ∂Ω du domaine Ω.
Une fois cette étude menée à bien on pourra envisager la résolution de l’équation de Navier-Stokes en utilisant une méthode itérative qui consiste à résoudre une succession de problèmes linéaires de Stokes.
Pour ne pas alourdir l’exposé on suppose que les principes de base de la méthode des éléments finis sont connus. Ces principes sont exposés dans [AF 503] [AF 504] [AF 505] et permettent une étude préalable de cette méthode.
Cet article est divisé en quatre grandes parties. La première présente la résolution des équations de Stokes par la méthode des éléments finis ; l’étude de cette partie est essentielle pour la compréhension des suivantes. On présentera donc dans cette partie la formulation variationnelle du problème de Stokes puis la discrétisation par éléments finis avec une présentation d’éléments finis admissibles ; on terminera en donnant quelques estimations d’erreurs. La deuxième partie est consacrée à la résolution des équations de Navier-Stokes par la méthode des éléments finis ; en particulier on donnera quelques estimations d’erreurs et on indiquera quelques méthodes de résolution du système discrétisé, ces méthodes étant distinctes de celles présentées dans [AF 1 404] ; on indiquera brièvement des procédés de discrétisation temporelle par éléments finis. La partie suivante est consacrée à la résolution des équations de Navier-Stokes discrétisées par la méthode de pénalisation et par la méthode d’Uzawa et ses variantes, en particulier la méthode du lagrangien augmenté. La dernière partie constitue une conclusion des méthodes présentées dans [AF 1 404] [AF 1 406] comparées à celles présentées dans cet article. Après avoir évoqué quelques grands types d’applications, on indiquera quelques généralités sur les méthodes de résolution des équations de Navier-Stokes en précisant notamment la structure d’un code de mécanique des fluides ; puis on décrira des codes industriels basés, d’une part, sur l’utilisation des volumes finis et, d’autre part, sur celle des éléments finis, ce qui permettra de dégager quelques critères de choix vis-à-vis de l’utilisation de l’une ou l’autre de ces méthodes.
Après une conclusion générale cet article sera complété par deux annexes, la première permettant de rappeler la définition de quelques espaces fonctionnels, en particulier les espaces de Sobolev ainsi que les propriétés de ces espaces, tout au moins les plus simples, et la seconde annexe rappelant le théorème de la divergence et la formule de Green adaptée à la mise sous forme variationnelle des équations de Stokes et de Navier-Stokes.
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Mathématiques
(170 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
2. Résolution des équations de Navier-Stokes par la méthode des éléments finis
2.1 Quelques résultats abstraits
On considère pour simplifier l’équation de Navier-Stokes incompressible bidimensionnelle munie des conditions aux limites de Dirichlet homogènes (C.L.) :
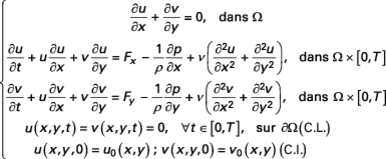
où Ω est un ensemble ouvert borné régulier de
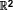 et T représente l’horizon en temps ; u0 et v0 représentent les conditions initiales (C.I.).
et T représente l’horizon en temps ; u0 et v0 représentent les conditions initiales (C.I.).
Comme pour le problème de Stokes, pour la seconde formulation variationnelle, on définit le problème variationnel associé dans l’espace des fonctions test J0( Ω) défini comme précédemment par :
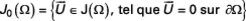
avec
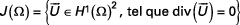
On a donc le problème suivant à résoudre :
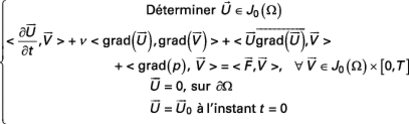
avec
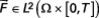 . On pose :
. On pose :
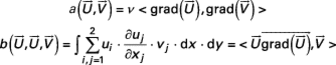
et on obtient l’expression suivante du problème variationnel :
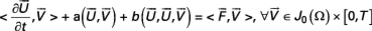
car en appliquant la formule de Green (voir annexe 2 § ...
Cet article fait partie de l’offre
Mathématiques
(170 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Résolution des équations de Navier-Stokes par la méthode des éléments finis
BIBLIOGRAPHIE
-
(1) - AXELSON (O.), BARKER (V.A.) - Finite element solution of boundary value problems - Theory and computation. - Academic press. 6 (1984).
-
(2) - BARANGER (J.) - Analyse numérique, - Hermann (1991).
-
(3) - BRUNEAU (C.H.) - Sixteenth international conference on numerical methods in fluid dynamics, - Springer (1998).
-
(4) - CHERRUAULT (Y.), LORIDAN (P.) - Modélisation et méthodes mathématiques en bio-médecine, - Masson (1977).
-
(5) - CIARLET (P.G.) - Numerical analysis of the finite element méthod, - Les presses de l’Université de Montréal (1976).
-
(6) - CIARLET (P.G.) - Introduction à l’analyse numérique matricielle et à l’optimisation. - Collection Mathématiques...
DANS NOS BASES DOCUMENTAIRES
Cet article fait partie de l’offre
Mathématiques
(170 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive










