Présentation
RÉSUMÉ
Dans le cadre de la sûreté de fonctionnement des systèmes, cet article aborde les moyens d’étude expérimentale de test des équipements et de traitement des données utilisées en fiabilité. L’estimation statistique des fautes aléatoires dépend de plusieurs paramètres, dont les lois de distribution des événements retenus, la phase à valider et les méthodes de collecte des données. Sont détaillés les plans d’essai standards de conformité à une spécification, l’analyse du taux de défaillance par la distribution de Weibull, ainsi que les méthodes de traitement lors d’essais incomplets.
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleAuteur(s)
-
Marc GIRAUD : Ingénieur de l’École Française de Radioélectricité, d’Électronique et d’Informatique (EFREI) - Ancien chef du service sûreté de fonctionnement et testabilité de Dassault Électronique
INTRODUCTION
Après les moyens d’étude théorique de la sûreté de fonctionnement, en phase de conception, on en vient ici aux méthodes de test des équipements et de traitement des données utilisées en fiabilité lors du développement et de l’exploitation, vis-à-vis des seules fautes aléatoires.
Les procédures dépendent de multiples paramètres : lois gouvernant la distribution des événements auxquels on s’intéresse (nombre de pannes ou instants d’apparition), éthique statistique dans laquelle on se place (« classique » ou bayésienne), phase industrielle à valider (développement, production, exploitation), méthodes de collecte etc. qui constituent autant d’options à considérer. Plusieurs problèmes sont abordés :
-
l’estimation ponctuelle et l’encadrement du
![]() constant (ou du MTTF θ) d’une population, à partir d’essais limités – par censure du nombre d’échecs ou troncature du temps – en statistique classique puis bayésienne ;
constant (ou du MTTF θ) d’une population, à partir d’essais limités – par censure du nombre d’échecs ou troncature du temps – en statistique classique puis bayésienne ; -
la sanction continue, à risques partagés, du niveau qualité d’un lot, ou de tenue d’un MTTF contractuel par plans d’essai standards (§ 2.1 à § 2.5) ;
-
l’analyse (Weibull) de populations présentant un λ variable dans le temps ;
-
l’estimation de paramètres d’une distribution inconnue à partir de données opérationnelles incomplètes (non datées/non explicitées ou sous-échantillonnées) recueillies sur site (§ 4.1 à § 5.3).
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Électronique
(228 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
5. Méthodes de traitements pour essais incomplets [3]
Par essais incomplets, il faut entendre les méthodes que les anglo-saxons appellent « suspended item testing » et « sudden death testing ».
La première ne demande pas de connaître la datation des événements, mais seulement la cause (panne ou suspension) de l’arrêt et le rang probable dans l’ordre d’arrivée, dont on examinera d’abord l’incidence.
La seconde vise à réduire le temps d’essai en analysant le seul échantillon, objet des pannes, dont on connaît ici la datation donc le rang.
Ces cas se rencontrent fréquemment en pratique, par exemple s’il faut analyser des résultats avant la fin programmée d’une période d’un contrat (suite à des performances inattendues), ou si on analyse les résultats d’un parc de matériels mis en service à différentes époques.
5.1 L’approximation de F (x) sur petits échantillons : rangs moyens et rangs médians
Quand il n’y a pas de regroupements possibles des événements en classes, on affecte à chaque observation un ordre croissant de survenue : son rang i, et on assimile la fonction de répartition empirique F (x) à la valeur cumulée : i /n.
Or, avec cette approximation de la fonction de répartition, à la nème observation de l’échantillon la fonction vaudra 1, alors que pour la population mère, cela ne se produirait qu’après un nombre x → ∞.
Pour corriger cette erreur on utilise des estimateurs, fonction de l’ordre i.
Soit un échantillon de la VA x (date de panne). Si on note Zi, n le rang vrai de la i ème observation dans n, on démontre que ce rang vrai peut s’estimer par :
-
l’approximation du i ème rang moyen :
![]()
ou mieux par :
-
l’approximation du i ème rang médian :
![]()
Cet article fait partie de l’offre
Électronique
(228 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Méthodes de traitements pour essais incomplets [3]
BIBLIOGRAPHIE
-
(1) - MIL-HDBK-781 D - Reliability Testing for Engineering Development, Qualification and Production. - D.O.D Washington D.C (1983).
-
(2) - BONIS (A.J.) - Why Bayes is better. - Proceedings Annual Reliability and Maintainability Symposium (1975).
-
(3) - T.E.B.A.L.D.I/marché aérospatiale 20811-3016 - Méthode pour l’évaluation et la construction de la fiabilité des équipements électroniques et électromécaniques - . ESD, Électronique Serge Dassault (1985).
Cet article fait partie de l’offre
Électronique
(228 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive









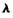 constant (ou du MTTF θ) d’une population, à partir d’essais limités – par censure du nombre d’échecs ou troncature du temps – en statistique classique puis bayésienne ;
constant (ou du MTTF θ) d’une population, à partir d’essais limités – par censure du nombre d’échecs ou troncature du temps – en statistique classique puis bayésienne ;


