Présentation
RÉSUMÉ
Les systèmes réparables constituent encore la majeure partie de l’électronique. Leurs caractéristiques de sûreté de fonctionnement portent sur l’indisponibilité, la probabilité pour que l’entité soit inapte à l’utilisation, et le taux de défaillance élémentaire, la fréquence des défaillances, permettant de dimensionner la logistique de soutien. Seule la modélisation du cycle du processus de fonctionnement et de maintenance curative rend compte du cycle de vie du système et permet les calculs des probabilités d’état. Les cas de figure sont nombreux, plusieurs méthodes analytiques permettent d’y répondre. Des exemples ont été retenus pour illustrer ces modélisations qualitatives de fonctionnement et de dysfonctionnements.
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleAuteur(s)
-
Marc GIRAUD : Ingénieur de l’École Française de Radioélectricité, d’Électronique et d’Informatique (EFREI) - Ancien chef du service Sûreté de fonctionnement et Testabilité de Dassault Électronique
INTRODUCTION
Les systèmes réparables constituent encore la majeure partie de l’électronique (mis à part les dispositifs dont le coût de réparation est prohibitif devant celui de fabrication).
Sur leur cycle de vie, les caractéristiques SdF les plus pertinentes y sont celles qui grèvent le coût de possession, c’est-à-dire l’indisponibilité et le taux de défaillance élémentaire.
La première s’exprime – ponctuellement – par la probabilité pour que l’entité considérée soit inapte à l’utilisation (malgré la redondance éventuelle et les réparations), ou bien – après stabilisation du régime transitoire – par le temps moyen après lequel le matériel n’est plus utilisable (entre défaillance et remise en service).
Le second rend compte de la fréquence des défaillances, qui devient vite constante et permet – de préférence à la fiabilité – de dimensionner la logistique de soutien.
Mais c’est la modélisation même du processus de fonctionnement et de maintenance curative qui rend compte du cycle de vie du système et permet les calculs des probabilités d’état ou de ses estimateurs.
Plusieurs méthodes analytiques sont présentées pour répondre aux différents cas de figure :
-
d’abord (et plus en profondeur, car la plus utilisée) celle dite MEE (méthode de l’espace des états) pour le processus markovien à taux de transition
![]() et
et
![]() constants ; ensuite, brièvement, quelques-unes de ses extensions : états fictifs, états de marche critique et séquences d’états ;
constants ; ensuite, brièvement, quelques-unes de ses extensions : états fictifs, états de marche critique et séquences d’états ; -
enfin, sa généralisation aux processus semi-markoviens où la probabilité de transition d’un état vers un autre ne dépend que du temps de séjour écoulé dans le premier.
Toutefois, ces analyses séquentielles ne permettent pas de modéliser les situations de conflit ou de blocage, survenant particulièrement dans les systèmes asynchrones.
On présente donc dans la suite, à l’aide de la symbolique très riche des réseaux de Petri (RdP), des exemples – parmi bien d’autres – de modélisations qualitatives de fonctionnement et de dysfonctionnements. On en vient enfin à leur utilisation quantitative (RdPS), via l’équivalence markovienne, par le choix approprié de lois de tirage des transitions du réseau ou comme support bas niveau pour simulations de Monte-Carlo.
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Électronique
(235 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
2. Cas où et dépendent de l’état du système : méthode de l’espace des états
La Méthode de l’Espace des États MEE, fondée sur les chaînes de Markov homogènes (à taux de transition constants dans le temps) décrit de manière causale et analytique l’évolution d’un système quelconque, réparable, en particulier si le nombre de réparateurs est inférieur au nombre d’entités qui le composent. On généralise ici le raisonnement du § 1 présenté ici sous forme matricielle.
2.1 Étapes et principe de la MEE
Pour calculer la fiabilité ou la disponibilité d’un système dont les taux de hasard hij (défaillance
 , réparation
, réparation
 , ou défaillance à la sollicitation
, ou défaillance à la sollicitation
 ) ne dépendent QUE de l’état où il se trouve, indépendamment du passé, il faut :
) ne dépendent QUE de l’état où il se trouve, indépendamment du passé, il faut :
• Recenser et identifier les n états Ei (opérationnels ou non) occupés par le système au cours de son évolution dans le temps.
• Tracer le graphe sagittal des transitions possibles entre états, exclusifs les uns des autres.
• Affecter les taux de hasard hij convenant à celles-ci, et écrire la matrice H des taux associés au graphe du problème posé (fiabilité ou disponibilité).
• Calculer les probabilités instantanées du vecteur d’état, en intégrant le système différentiel :
Cet article fait partie de l’offre
Électronique
(235 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Cas où et dépendent de l’état du système : méthode de l’espace des états
BIBLIOGRAPHIE
-
(1) - GONDRAN (M.), PAGÉS (A.) - Fiabilité des systèmes. - Collection de la direction des études et recherches d’EDF, Eyrolles (1980).
-
(2) - VILLEMEUR (A.) - Sûreté de fonctionnement des systèmes industriels. - Eyrolles (1988).
-
(3) - LEROY (A.), SIGNORET (J.–P.) - Le risque technologique. - Que sais-je ? no 2669, PUF.
-
(4) - AGERWALA (T.K.) - Putting Petri nets to work. - IEEE (1979).
-
(5) - HURA (G.S.) - Petri net as a modelling tool. - Microelectronics Reliability, vol. 22, no 3 (1982).
-
(6) - HURA (G.S.) - Petri net approach to the analysis of a stuctured program. - Microelectronics Reliability, vol. 22, no 3 (1982).
-
...
Cet article fait partie de l’offre
Électronique
(235 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive









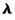 et
et
 constants ; ensuite, brièvement, quelques-unes de ses extensions : états fictifs, états de marche critique et séquences d’états ;
constants ; ensuite, brièvement, quelques-unes de ses extensions : états fictifs, états de marche critique et séquences d’états ;
