Bibliographie & annexes
Présentation
En anglais
Auteur(s)
-
Stéphane FONT : Enseignant‐chercheur à l’École supérieure d’électricité, à Gif‐sur‐Yvette
-
Gilles DUC : Professeur à l’École supérieure d’électricité, à Gif‐sur‐Yvette
-
François CARRÈRE : Ingénieur à la Société de mécanique magnétique (S2M), à Saint‐Marcel
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleINTRODUCTION
La synthèse H∞ prend une place de plus en plus importante parmi les méthodes de calcul de correcteur. Sa principale caractéristique est de permettre de modeler différents transferts d’un système asservi, tout en garantissant la stabilité de la boucle fermée. Elle permet également la prise en compte de certains objectifs de robustesse, tels que la garantie de marges de stabilité ou la robustesse aux dynamiques hautes fréquences mal connues ou non modélisées.
Nous avons mis en œuvre cette approche, dans le but de développer une méthodologie permettant la synthèse de régulateurs pour des paliers magnétiques. Il s’agit d’un problème qui comporte des spécifications nombreuses et très précises. Dans de nombreux cas, il peut être résolu par des méthodes classiques, mais pas de façon systématique, d’où un temps de conception plus long. Il est par ailleurs difficile de faire des campagnes d’essais pour optimiser un aspect particulier du cahier des charges.
Pour concevoir la commande, nous avons utilisé le modèle d’un rotor flexible sous forme modale, qui comporte, en plus de l’inertie, six modes de flexion. La synthèse est préalablement réalisée en continu. Une synthèse discrète est ensuite effectuée, en utilisant la transformée en w.
Dans le paragraphe 1, nous expliquons les principes de la synthèse H ∞ . Le paragraphe 2 présente le système physique et son modèle, ainsi que le cahier des charges traité. La synthèse H ∞ est décrite dans le paragraphe 3, en indiquant comment sont prises en compte les spécifications (bande passante, rejet des perturbations, amortissement des modes, filtrage haute fréquence). Ce paragraphe se termine par une réduction d’ordre du correcteur obtenu. Enfin, la démarche générale est reproduite au paragraphe 4 pour obtenir un correcteur numérique.
L'expertise technique et scientifique de référence
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Le contrôle des paliers magnétiques
En anglais
1. Synthèse H ∞
1.1 La norme H∞
Tout système linéaire et invariant peut être modélisé par une fonction de transfert ou transmittance H (p ). Si le système a q entrées et r sorties, H (p ) est une matrice r × q. Dans le cas où le système est stable, on définit sa norme H ∞ par :
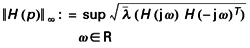
où la notation
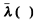désigne la plus grande des valeurs propres.
Pour un système à une entrée et une sortie, cette expression devient :
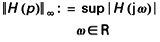
La norme H ∞ apparaît alors comme le maximum du module de la réponse fréquentielle.
HAUT DE PAGE1.2 Analyse des principaux transferts d’un asservissement
Considérons le schéma‐bloc de la figure 1, où G (p ) est un modèle sous forme de fonction de transfert du système à asservir et K (p ) est le correcteur ; r et d sont respectivement la référence et une perturbation reçue en entrée du système ; u est la commande élaborée par le correcteur et y la sortie à asservir ; ε est l’erreur d’asservissement.
On peut, à partir de ce schéma, exprimer la transformée de Laplace de l’erreur en fonction des transformées de Laplace des signaux appliqués :
d’où :
...
L'expertise technique et scientifique de référence
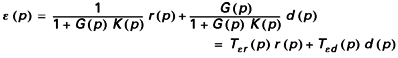Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Synthèse H ∞
BIBLIOGRAPHIE
-
(1) - BALAS (G.J.), DOYLE (J.C.), GLOVER (K.), PACKARD (A.), SMITH (R.) - The µ-analysis and synthesis toolbox, - Math Works Inc. (1993).
-
(2) - DOYLE (J.C.) - Analysis of Control Systems with Structured Uncertainty. IEE Proc. Part D, - vol. 129, pp. 242‐250 (1982).
-
(3) - DUC (G.) - Robustesse des Systèmes Linéaires Multivariables. - Polycopié Supélec no 03317 (1994).
-
(4) - DUC (G.) - Analyse de robustesse et synthèse d’une commande dans le cadre H∞ . in Systèmes de Régulation, - A. Rachid éditeur, Masson, p. 152‐187 (1996).
-
(5) - GLOVER (K.), DOYLE (J.C.) - State‐space formulae for all stabilizing controllers that satisfy an H∞‐norm bound and relations to risk sensitivity. - Systems & Control Letters, vol. 11, p. 167‐172 (1988).
-
(6) - FONT (S.) - Méthodologie...
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
