Bibliographie & annexes
Présentation
RÉSUMÉ
Au-delà d’une première approche et l’exécution de calculs simples, l’utilisation d’un système de calcul formel nécessite une connaissance approfondie du système et de ses limitations. En précisant les domaines des mathématiques où ce type de calcul présente un fort intérêt, cet article répond à la question de l’utilité d’un investissement dans une formation sur le calcul formel. De nombreux exemples illustrent son fonctionnement, et abordent ainsi ses calculs de base, notamment sur la dérivation, la simplification de formules et les tracés de courbes, mais aussi les calculs intégral et matriciel et la résolutions d’équations non linéaires. Pour cette présentation, c’est le système de calcul formel Maple qui a été choisi, ce système largement diffusé dispose d’une bibliothèque très riche et ouverte.
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleABSTRACT
Beyond an initial approach and the carrying out of simple calculations, the use of a formal calculation system requires an in-depth knowledge of the system and its limitations. By precising the mathematical domains where this type of calculation presents a significant interest, this article responds to the question of whether investment in formal calculation training is useful. Numerous examples illustrate its operation mode and thus deal with its basic calculations, notably on derivation, simplification of formulae and curve drawing, but also integral and matrix calculation and the resolution of non-linear equations. The formal calculation system Maple was selected for this presentation, as this widely diffused system has an extremely rich and open library.
Auteur(s)
-
Claude GOMEZ : Directeur de recherche INRIA (Institut national de recherche en informatique et en automatique)
-
Bruno SALVY : Directeur de recherche INRIA
INTRODUCTION
Le calcul formel est aujourd'hui très connu dans le monde scientifique en général et chez les ingénieurs en particulier. En effet, de nos jours, il est aisé d'installer et d'utiliser un système de calcul formel sur un simple micro-ordinateur à faible coût (PC, Macintosh). Lorsque l'on vient d'acquérir un tel système, il faut apprendre à l'utiliser. Dans un premier temps, il est très facile de réaliser des calculs simples, du style « calculatrice formelle », mais pour aller plus loin, une certaine connaissance du système et de ses limitations s'avère nécessaire. Sinon, l'utilisateur se décourage vite et abandonne. Donc, du temps de formation est indispensable à l'utilisation d'un système de calcul formel.
Une question apparaît alors : « le calcul formel est-il utile pour moi ? » ; autrement dit, « est-il rentable pour moi de passer du temps à apprendre à utiliser un tel système ? ». Le but de cet article est de répondre à cette question. Pour cela, nous allons passer en revue les principaux domaines des mathématiques dans lesquels le calcul formel peut résoudre des problèmes. Ces domaines sont ceux où l'ingénieur a généralement à travailler : les calculs sur les nombres et les fractions rationnelles, la dérivation, la simplification de formules et les tracés de courbes qui sont la base de tout système de calcul formel, mais aussi les calculs intégral et matriciel, la résolution d'équations non linéaires et des systèmes d'équations différentielles couramment utilisées par les ingénieurs. Et enfin, il faudra parler du calcul numérique. Ce dernier est en général la fin du travail de l'ingénieur et il ne faut pas opposer calcul formel et calcul numérique. Nous montrerons en effet les cas où le calcul formel peut s'avérer très utile dans ce domaine. Pour chaque partie, nous montrerons ce que sait faire le calcul formel, comment il le fait et quelles sont ses limitations.
Un grand nombre d'exemples émaillent ce document, ceci afin de montrer le fonctionnement du calcul formel à travers un système. Nous avons choisi le système de calcul formel Maple pour cela. La raison en est que ce système est très largement diffusé (comme Mathematica), qu'il dispose d'une bibliothèque suffisamment riche et ouverte (le code source de la plupart des fonctions est accessible) et qu'il est aisément extensible.
Le fonctionnement d'un système de calcul formel comme Maple est simple : l'utilisateur entre une commande, terminée par un point-virgule « ; » dans une syntaxe très naturelle, et Maple affiche la réponse en format haute résolution qui ressemble à la typographie mathématique. Si l'on remplace le point-virgule par un deux-points « : », la réponse n'est pas affichée. Maple utilise le principe des packages, c'est-à-dire qu'un grand nombre de commandes sont classées en groupes de même fonctionnalité. Dans ce cas, l'appel de la commande s'écrit <nom du package> [<nom de la commande>], comme LinearAlgebra [Determinant].
Le but de cet article n'est pas la description du système de calcul formel Maple. Nous n'expliquerons pas de façon détaillée la syntaxe et le fonctionnement de ce système. Pour cela, le lecteur est invité à consulter l'article « Calcul formel avec Maple » [H 3 028]. Mais les exemples ont été choisis pour qu'ils soient compréhensibles par le lecteur ; des explications seront données chaque fois que cela sera nécessaire.
L'expertise technique et scientifique de référence
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Mathématiques
(166 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Calcul intégral1. Calculs de base
La plupart des systèmes de calcul formel partagent les mêmes fonctionnalités de base, qui permettent de les utiliser comme des « calculettes formelles ». Dans ce mode, tous les calculs simples, formels ou numériques, qu'il s'agisse de calculs de dérivées, d'intégrales, de tracés de courbes ou de surfaces, sont résolus de façon aussi conviviale que possible.
1.1 Nombres
La caractéristique première du calcul formel est de manipuler des nombres entiers et rationnels exacts, à la différence des langages de programmation habituels (C ou Fortran) où ces nombres sont approchés ou tronqués lorsque leur taille dépasse celle d'un ou de deux mots machine.
Un calcul typique de nombres entiers est le calcul de la factorielle. Ci-après, nous calculons 100 ! en Maple. Il s'agit de simples multiplications où la seule difficulté est la grande taille des objets manipulés. À l'inverse, la fonction ifactor permet la décomposition d'un entier en ses facteurs premiers. L'efficacité de cette opération requiert des algorithmes sophistiqués, et fait encore l'objet de recherches actives, notamment du fait de ses applications en cryptographie.
La variable « % » fait référence au résultat calculé précédemment.
>100 ! ;
>ifactor (%) ;
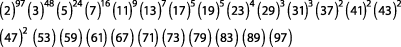
Les calculs de nombres de combinaisons et d'arrangements sont aussi faciles à réaliser en utilisant des nombres rationnels. Par exemple, la probabilité de gagner le gros lot au loto est l'inverse du nombre de tirages possibles, sachant qu'un tirage consiste à tirer 6 boules parmi 49 :
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Mathématiques
(166 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Calculs de base
BIBLIOGRAPHIE
-
(1) - VON ZUR GATHEN (J.), GERHARD (J.) - Modern Computer Algebra. - Cambridge University Press (1999).
-
(2) - GOMEZ (C.), SALVY (B.), ZIMMERMANN (P.) - Calcul formel : mode d'emploi, exemples en Maple. - 2e tirage avec mise à jour Maple V.4, Masson, Paris (1995).
-
(3) - JEANNEAU (X.) - Calcul formel avec Maple. - [H 3 028], Technologies logicielles – Architectures des systèmes (2002).
-
(4) - VIOLANTE (A.) - Documents mathématiques. Besoins et outils. - [H 7 167], Documents numériques – Gestion de contenu (2004).
-
(5) - VIOLANTE (A.) - Documents mathématiques. Norme MathML. - [H 7 168], Documents numériques – Gestion de contenu (2004).
-
(6) - GOMEZ (C.) - Scilab, un logiciel libre de calcul scientifique. - [IN 31], Mathématiques...
ANNEXES
(liste non exhaustive)
Axiom
http://www.axiom-developer.org
Maple
Mathematica
http://www.wolfram.com/mathematica
Scilab
HAUT DE PAGE
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Mathématiques
(166 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
