Présentation
RÉSUMÉ
L'objectif de l'article est de donner une introduction aux mathématiques de l'assurance. Après une brève présentation des opérations d'assurance et du problème de la solvabilité des entreprises d'assurances, l'accent est mis sur les principes théoriques de calcul des primes, les mesures de risque et sur le modèle collectif, alias modèle fréquence-coût, référence de base pour les actuaires. Dans ce cadre, on présente plusieurs méthodes d'évaluation ou d'approximation, de la prime d'assurance et, plus généralement, de la loi de probabilité du montant cumulé annuel des sinistres, ce qui doit permettre à l'assureur de mieux estimer l'ordre de grandeur de la sinistralité future et de constituer des provisions suffisantes.
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleAuteur(s)
-
Christian HESS : Professeur émérite - Membre de l’Institut des Actuaires - Université Paris Dauphine PSL, Paris, France
INTRODUCTION
L’importance économique de l’assurance ne cesse de croître dans les pays développés. Les assureurs proposent régulièrement à leurs clients de nouveaux types de contrats permettant de couvrir de nouveaux risques ou d’améliorer la couverture de risques déjà connus. Cela suppose une ingénierie assurantielle constamment mise à jour et susceptible de prendre en compte les différentes facettes de cette activité qui fait appel à plusieurs disciplines ou techniques, telles que les mathématiques, la statistique, le droit, l’économie, la comptabilité… Dans cet article traitant des mathématiques de l’assurance, on s’intéressera à des aspects quantitatifs qui sont traditionnellement pris en charge par les actuaires, ingénieurs spécialisés dans les techniques assurantielles et financières. L’étendue du sujet, dont on peut se convaincre par le nombre de publications et de références sur le Web, impose de se limiter à quelques thèmes importants.
Toute opération d’assurance commence par la signature d’un contrat entre un assureur et un assuré. Ce contrat prévoit un paiement immédiat et certain, la prime d’assurance, en échange d’un paiement futur et aléatoire qui sera concrétisé par des indemnités versées à l’assuré en compensation des sinistres survenus pendant la période de validité du contrat.
Il y a donc transfert de risque de l’assuré à l’assureur. La viabilité de cette opération n’est possible que par la mutualisation de nombreux risques au sein de l’entreprise d’assurance, ce qui permet une certaine compensation statistique, sans toutefois éliminer complètement les fluctuations du montant total des sinistres, objet des paiements futurs. Il en résulte que le risque supporté par l’assureur nécessite d’abord l’évaluation de la prime qui doit être suffisante pour faire face au coût moyen des sinistres, ainsi qu’aux fluctuations possibles de ce coût. Ces fluctuations, si elles sont d’amplitude exceptionnelles et défavorables, peuvent avoir un impact sur l’équilibre des comptes annuels de l’assureur, voire mettre en danger sa solvabilité. C’est pourquoi, ce dernier ne se contente pas d’évaluer la prime mais s’efforce également d’estimer la loi de probabilité du montant cumulé des sinistres dont la prime, malgré son importance, n’est qu’un indicateur parmi d’autres.
Dans cet article on examinera le problème de l’évaluation de la prime, qui est basée non seulement sur l’analyse de la sinistralité passée, mais aussi sur les principes théoriques de calcul de prime que l’assureur est susceptible de choisir en fonction de critères qui lui sont propres, notamment de son attitude face au risque. Concernant la loi de probabilité du montant cumulé des sinistres, étant donné la taille importante des portefeuilles de risques gérés par les entreprises d’assurances, les méthodes élémentaires d’évaluation, basées sur les convolutions, sont d’un emploi limité. L’actuaire doit alors se tourner vers des méthodes d’approximation ou des algorithmes spécifiques plus performants, tels que la méthode récursive de Panjer ou la transformation de Fourier rapide. La méthode de Monte-Carlo, basée sur la génération d’échantillons aléatoires sur ordinateur, est aussi largement utilisée dans le milieu professionnel.
Dans la dernière partie, on revient sur la notion de prime qui peut présenter deux modalités : la prime a priori et la prime a posteriori. Comme son nom l’indique, la prime a priori est payée par l’assuré à la signature du contrat et est déterminée à partir des caractéristiques du risque assuré. En assurance automobile, l’assureur se basera par exemple sur la puissance du véhicule, la zone d’utilisation, l’ancienneté du permis du conducteur… En assurance habitation, ce sera la superficie et la situation des locaux assurés… La prime a posteriori, quant à elle, va dépendre de la sinistralité observée et est donc susceptible de varier d’une année à l’autre et d’un risque à l’autre à l’intérieur du même groupe de risques. L’exemple le plus connu est celui de l’assurance responsabilité civile pour le conducteur d’un véhicule à moteur. Plusieurs modèles rendent possibles l’évaluation de ce type de prime. On se limitera ici à un exemple simple basé sur une approche bayésienne.
En fin d’article, on trouvera des références bibliographiques et des liens vers des sites ou documents numériques qui devraient permettre au lecteur intéressé d’approfondir certains des thèmes présentés.
MOTS-CLÉS
solvabilité mesures de risque prime d'assurance tarification d'expérience modèle collectif
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Mathématiques
(170 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
3. Notion de mesure de risque
Une notion apparentée à celle de principe de calcul de prime, mais plus générale, est celle de mesure de risque, définie comme une application
 de l’ensemble des risques à valeurs dans
de l’ensemble des risques à valeurs dans
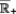 . Pour un risque X, ρ(X) peut représenter la prime technique permettant de couvrir le risque, de sorte que tous les principes de calcul de prime présentés précédemment sont des mesures de risques possibles. Mais ρ(X) peut aussi représenter le montant minimal, incluant prime et réserve affectée au risque dont doit disposer l’assureur pour couvrir le risque X durant la période de référence. De ce point de vue, le coefficient de sécurité, défini en (9), se présente aussi comme un mesure de risque. On introduit généralement la condition de normalisation ρ(0) = 0.
. Pour un risque X, ρ(X) peut représenter la prime technique permettant de couvrir le risque, de sorte que tous les principes de calcul de prime présentés précédemment sont des mesures de risques possibles. Mais ρ(X) peut aussi représenter le montant minimal, incluant prime et réserve affectée au risque dont doit disposer l’assureur pour couvrir le risque X durant la période de référence. De ce point de vue, le coefficient de sécurité, défini en (9), se présente aussi comme un mesure de risque. On introduit généralement la condition de normalisation ρ(0) = 0.
Quelques exemples sont présentés ci-après. D’abord la valeur risquée, ou Value at Risk, qui fournit une valeur de X ayant une forte probabilité de ne pas être dépassée. Le deuxième exemple présente en fait plusieurs mesures de risques apparentées qui donnent le coût moyen des sinistres ou la perte moyenne dans le cas, peu probable mais non impossible, où la valeur risquée est dépassée. Le troisième exemple, le déficit attendu, reprend la même idée sans conditionnement.
3.1 Valeur risquée
Étant donné un risque X et
 la valeur risquée (ou Value at Risk) de X au niveau α est noté Var(X ; α) et définie, lorsque FX est inversible, comme la solution unique de l’équation en x
la valeur risquée (ou Value at Risk) de X au niveau α est noté Var(X ; α) et définie, lorsque FX est inversible, comme la solution unique de l’équation en x
 ...
...Cet article fait partie de l’offre
Mathématiques
(170 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Notion de mesure de risque
BIBLIOGRAPHIE
-
(1) - ABRAMOBITZ (M.), STEGUN (I.A.) - Handbook of Mathematical Functions – Formulas, Graphs and Mathematical Tables. - National Bureau of Standards Applied Mathematical Series, # 55 (10e réimpression en décembre 1972, Version téléchargeable disponible), Juin 1964.
-
(2) - ARTZNER (Ph.), DELBAEN (F.), EBER (J.-M.), HEATH (D.) - Coherent risk measures – - Mathematical Finance 9, 203-228 (1999).
-
(3) - BEARD (R.), PENTIKAÏNEN (T.), PESONEN (E.) - Risk Theory - (3e édition), Chapman et Hall (1984).
-
(4) - BLONDEAU (J.), PARTRAT (P.) - La réassurance – Approche technique, - Economica (2003).
-
(5) - BÜHLMANN (H.) - Mathematical methods in risk theory, Springer - (1970).
-
(6) - BÜHLMANN (H.), GISLER (A.) - A...
ANNEXES
Lien vers le site Assurance et Mutuelle : les branches de l’assurance
https://www.assurance-et-mutuelle.com/assurance/ branches-assurance.html
Lien permettant de télécharger l’ouvrage Handbook of Mathematical Functions – Formulas, Graphs and Mathematical Tables, par Abramobitz M. et Stegun I.A.
https://personal.math.ubc.ca/~cbm/aands/abramowitz_and_stegun.pdf
Pour accéder au site de la Banque de France et au document sur la directive européenne Solvabilité 2
L’article de Géraldine Vial, paru dans L’Argus de l’assurance en juillet 2016 résume les principes de la directive Solvabilité 2 et les compare avec ceux de Solvabilité 1
https://www.argusdelassurance.com/acteurs/les-3-piliers-de-solvabilite-2-special-solva-2.109623
Pour télécharger le document Solvabilité II : une réforme inutile et dangereuse – Livre Blanc, rédigé par la Société de Calcul Mathématique SA, Avril 2016
http://www.scmsa.eu/archives/SCM_Solvability_II_2016_04.pdf
HAUT DE PAGECet article fait partie de l’offre
Mathématiques
(170 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive










