Présentation
Auteur(s)
-
Jean AUVRAY : Ingénieur de l’École nationale supérieure de physique chimie industrielle (ESPCI) - Docteur ès sciences - Professeur à l’Université Pierre-et-Marie-Curie (Paris-VI)
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleINTRODUCTION
On peut lire souvent que le filtrage numérique est une opération qui à une suite de nombre xn fait correspondre une autre suite de nombre yn. Cette définition, bien qu’exacte, masque le fait essentiel, à notre avis : l’important n’est pas la suite de nombres mais le signal, le plus souvent continu, qui est l’image du phénomène physique auquel s’attache l’expérimentateur.
Nous définirons donc ainsi le filtrage numérique : soit un signal
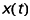 auquel on veut faire correspondre un signal
auquel on veut faire correspondre un signal
 résultant de
résultant de
 par un filtrage linéaire de fréquence. Le filtrage numérique est une opération sur les échantillons xn du signal
par un filtrage linéaire de fréquence. Le filtrage numérique est une opération sur les échantillons xn du signal
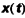 qui va conduire aux échantillons yn, lesquels devront permettre de reconstituer un signal aussi voisin que possible du signal
qui va conduire aux échantillons yn, lesquels devront permettre de reconstituer un signal aussi voisin que possible du signal
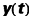 désiré.
désiré.
Nous pensons qu’il est nécessaire, pour aborder le filtrage numérique, de bien connaître le filtrage analogique (à temps continu), car le physicien raisonne le plus souvent sur des signaux continus et ce qu’il souhaite c’est un graphe plutôt qu’une suite de nombres (cf. [R 1 102]).
Il ne faut pas oublier que préalablement à tout échantillonnage il est indispensable d’effectuer sur le signal un filtrage préalable passe-bas (cf. [R 1 102]) (cf. § 1.4.2) pour éviter les repliements de spectre. Plus le filtre numérique est précis, plus le filtre antirepliement doit être élaboré. Cependant la puissance des circuits numériques actuels est telle que le filtre analogique de tête est de plus en plus souvent supprimé, il suffit d’échantillonner assez vite le signal brut à la sortie du capteur pour respecter approximativement le théorème de Shannon (rappelé au § 1.1), puis effectuer ensuite un filtrage passe-bas numérique.
Après un court paragraphe sur les outils mathématiques nécessaires, nous aborderons les filtres transversaux, à réponse impulsionnelle finie (§ 2) qui présentent les caractéristiques suivantes :
-
ils présentent l’avantage d’être toujours stables ;
-
leur déphasage peut être rendu proportionnel à la fréquence (retard de groupe constant) ;
-
une précision faible sur les coefficients est acceptable ;
-
leur synthèse est souvent assez simple et ils peuvent atteindre des puissances remarquables, bien au-delà de ce que l’on peut espérer de filtres analo-giques, mais lorsque le nombre de leurs coefficients augmente ils exigent une puissance de calcul importante.
Par suite de leur stabilité intrinsèque, ce sont des structures transversales qui sont choisies le plus souvent pour réaliser des filtres adaptatifs dont les coefficients s’ajustent dynamiquement pour optimiser à chaque instant les performances.
La détermination des coefficients des filtres numériques ne nécessite pas une grande puissance de calcul, une calculette programmable est parfois suffisante, mais des outils informatiques disponibles sur tous les micro-ordinateurs, par exemple un logiciel tel que EXCEL, apportent un confort bien plus grand et permettent même de simuler, en temps différé, le fonctionnement du filtre.
Cet article s’insère dans une série consacrée à la pratique du filtrage :
-
Pratique du filtrage. Introduction [R 1 100] ;
-
Pratique du filtrage. Filtrage analogique [R 1 102] ;
-
Pratique du filtrage. Filtrage numérique. Filtres transverses [R 1 105] ;
-
Pratique du filtrage. Filtrage numérique. Filtres récursifs [R 1 106].
VERSIONS
- Version archivée 1 de juil. 1988 par Jacques MAX
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Mesures et tests électroniques
(79 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
2. Filtres à réponse impulsionnelle finie
La valeur de sortie à l’instant n (
 ) est calculée à partir d’un nombre fini d’échantillons antérieurs d’entrée :
) est calculée à partir d’un nombre fini d’échantillons antérieurs d’entrée :

Le nombre de termes étant fini, il en est toujours de même de leur somme : un filtre transverse est donc toujours stable. Cette qualité est essentielle et permet de construire des filtres très complexes, par exemple les filtres adaptatifs que nous décrirons brièvement dans l’article [R 1 106] (§ 1.7), sans risque d’instabilité.
La fonction de transfert en z associée est un polynôme en
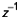 , l’absence de dénominateur, donc de pôles, est un gage de stabilité :
, l’absence de dénominateur, donc de pôles, est un gage de stabilité :

Nous avons vu au paragraphe 1.4.2 que les coefficients successifs du filtre sont les valeurs de la réponse impulsionnelle h échantillonnée à la fréquence
 .
.
L’algorithme de calcul du filtre peut donc se mettre sous la forme :
 ...
...Cet article fait partie de l’offre
Mesures et tests électroniques
(79 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Filtres à réponse impulsionnelle finie
Cet article fait partie de l’offre
Mesures et tests électroniques
(79 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Des modules pratiques
Opérationnels et didactiques, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive










