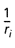Présentation
English
RÉSUMÉ
Cet article regroupe les formules et données utiles à l’appropriation du contenu de l’Eurocode 2EC2. Cette norme énonce les principes de base de calcul des structures en béton armé, non armé, et précontraint. Sont ainsi présentés les calculs en flexion à l’état-limite ultime (section rectangulaire sans aciers comprimés), ceux relatifs à la fissuration (section homogène non fissurée et fissurée), et deux méthodes de calcul approchées de la courbure d’une poutre.
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleAuteur(s)
-
Jean PERCHAT : Ingénieur des Arts et Manufactures - Professeur honoraire à l’École supérieure des travaux publics et au Centre des hautes études de la construction
INTRODUCTION
Dans ce dossier sont regroupées les formules et données utiles aux dossiers traitant de l’Eurocode 2. Béton armé :
-
[C 2 330] Dispositions et données générales ;
-
[C 2 331] Vérification des états-limites ultimes ;
-
[C 2 332] Vérification des états-limites de service.
L'expertise technique et scientifique de référence
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Les superstructures du bâtiment
(117 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Calculs en flexion à l’état-limite ultime (article 6.1 de l’EC2)
English
3. Flèches. Méthodes de calcul approchées
3.1 Méthode A
La poutre étant découpée en plusieurs tronçons égaux, on suppose que sur chaque tronçon la courbure varie linéairement. L’équation de la déformée est donc (double intégration) un polynôme du 3e degré.
La flèche a dans une section j est de la forme :
avec :
-
![]()
: - courbure dans les différentes sections limitant les tronçons, sections sur appuis comprises
- ki :
- coefficients des polynômes, déterminés en écrivant la continuité des courbures, des rotations et des flèches au droit de chaque section i
- N :
- coefficient fonction du nombre de sections considérées.
Cette méthode est applicable à une poutre continue, à condition d’affecter le signe « moins » aux courbures des sections où le moment est négatif.
Par exemple, pour 10 sections de calcul équidistantes de 0,1
, la flèche à mi-portée peut être déterminée en calculant :
avec
,
courbures dans les sections d’extrémité.
Pour un chargement symétrique, l’expression se simplifie et donne la flèche maximale à mi-portée :
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Les superstructures du bâtiment
(117 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Flèches. Méthodes de calcul approchées
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Les superstructures du bâtiment
(117 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
