Présentation
Auteur(s)
-
Gérard ALENGRIN : Professeur à l’Université de Nice Sophia Antipolis
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleINTRODUCTION
Cet article est consacré à la commande de systèmes physiques à l’aide d’un calculateur numérique.
C’est un vaste domaine de recherche, et l’on se limitera à l’étude des systèmes asservis pour lesquels on aura à définir différents types de correcteurs.
On peut voir, dans divers ouvrages sur les systèmes asservis linéaires continus, les principales propriétés de ces systèmes en boucle fermée, notamment en ce qui concerne la réduction de sensibilité aux perturbations ou aux variations de paramètres.
On peut également constater (voir que, pour obtenir des résultats satisfaisants en termes de réponse dynamique et de précision, une simple boucle de retour n’est souvent pas suffisante et qu’il faut ajouter un correcteur analogique.
Le développement considérable des calculateurs numériques a permis de les utiliser dans la commande en temps réel des systèmes.
Les principaux avantages de l’utilisation d’un calculateur numérique se situent au niveau d’une grande souplesse dans la programmation des algorithmes, ce qui permet d’obtenir facilement des lois de commandes variées. Ceci doit être comparé à la détermination de correcteurs analogiques, plus difficiles à réaliser physiquement.
L'expertise technique et scientifique de référence
VERSIONS
- Version archivée 1 de janv. 1986 par Claude BOZZO
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Automatique et ingénierie système
(139 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Annexe. Principaux résultats sur les équations polynomiales4. Synthèse de correcteurs numériques par les équations polynomiales
On a développé au paragraphe 3 des méthodes de recherche de correcteurs en z en s’appuyant sur la méthode du lieu des racines pour déterminer d’abord les paramètres de correcteurs classiques et ensuite des correcteurs utilisant la compensation de pôles et de zéros.
Dans ce paragraphe, on va décrire des méthodes plus systématiques de synthèse de correcteurs qui s’appuient sur la résolution d’équations polynomiales en z .
4.1 Méthode de Volguine
Dans cette partie, on choisira d’utiliser des polynômes en z –1 ce qui permet de simplifier certaines considérations (notamment en ce qui concerne les notions de causalité du correcteur et aussi pour la résolution des équations polynomiales).
On considère toujours le système représenté sur la figure 3.
HAUT DE PAGE
D’une manière générale,
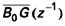se présente sous la forme d’un numérateur en z –1 et d’un dénominateur en z –1. On factorise sous la forme :
L'expertise technique et scientifique de référence
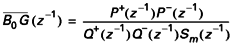
Cet article fait partie de l’offre
Automatique et ingénierie système
(139 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Synthèse de correcteurs numériques par les équations polynomiales
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Automatique et ingénierie système
(139 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
