Bibliographie & annexes
Présentation
En anglais
Auteur(s)
-
Marcel NOUGARET : Professeur à l’Université de Grenoble, Laboratoire d’Automatique
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleINTRODUCTION
La sortie du procédé que l’on commande doit évoluer pour suivre la consigne demandée. Il faut donc à tout instant (ou périodiquement en régulation numérique) appliquer, à l’entrée puissance du procédé, la commande appropriée. Cette commande est calculée par un ensemble de traitements d’informations, le correcteur, qui utilise des opérateurs (sommateurs, gains, intégrateurs, dérivateurs) élaborant la commande à partir du signal d’erreur et des mesures auxiliaires disponibles.
L'expertise technique et scientifique de référence
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Correction des procédés à dominante du deuxième ordre
En anglais
4. Correction des procédés à dominante du premier ordre
Nous considérons des procédés pour lesquels le gain g et la constante de temps τ ont été déterminés expérimentalement (essai en échelon par exemple) ou bien théoriquement, en ayant éventuellement négligé une seconde constante de temps, petite devant τ. Il faut noter en particulier que la réalité est représentée par le modèle
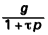mais qu’il ne peut s’agir que d’une représentation approximative, liée à une certaine échelle d’amplitude et de temps.
Il faut en conséquence, quand on veut fixer un temps de réponse désiré pour un système bouclé, garder à l’esprit que ce temps de réponse (asservi) doit être comparé avec celui du système non asservi et que leurs échelles de temps doivent être compatibles avec la précision des mesures du modèle dynamique en boucle ouverte.
Par exemple, si le modèle d’un processus comprend une constante de temps de 2 s et si les conditions expérimentales sont telles que l’on puisse ne pas avoir tenu compte d’une constante de temps 50 fois plus petite (0,04 s), il serait illusoire de vouloir calculer à partir du modèle approximatif (τ = 2 s) un asservissement dont le temps de réponse serait de l’ordre des constantes de temps négligées ; il est clair que le modèle serait utilisé ici en dehors de l’échelle de temps avec laquelle il a été établi.
4.1 Limitations pratiques du réglage par un gain
Nous nous proposons de montrer qu’un correcteur CE (p ) = K , bien que théoriquement satisfaisant pour un processus modélisé par un premier ordre, présente des risques d’instabilité en présence de constantes de temps négligées très faibles, et cela particulièrement quand on veut des erreurs faibles. De plus, il entraîne des commandes qui sont, en transitoire, beaucoup plus grandes que la commande permanente, provoquant ainsi un fonctionnement en régime saturé qui risque d’être très gênant.
HAUT DE PAGE
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Correction des procédés à dominante du premier ordre
BIBLIOGRAPHIE
-
(1) - DE CARFORT (F.), FOULARD (C.), CALVET (J.) - Asservissements linéaires continus. - Dunod (1976).
-
(2) - GILLE (J. Ch.), DECAULNE (P.), PÉLEGRIN (M.) - Dynamique de la commande linéaire. - Dunod (1967).
-
(3) - DE LARMINAT (P.), THOMAS (Y.) - Automatique des systèmes linéaires. - Tome 3, Commande, Flammarion Sciences (1977).
-
(4) - TAKAHASHI (Y.), RABINS (M.), AUSLANDER (D.) - Control. - Addison Wesley (1970).
-
(5) - DORF (R.) - Modern Control Systems. - Addison Wesley (1967).
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Automatique et ingénierie système
(138 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
