Bibliographie & annexes
Présentation
English
RÉSUMÉ
Sujet classique des mathématiques, le calcul des variations a fait couler beaucoup d'encre et sur un grand nombre d'échanges, les modèles proposés étant souvent exprimés en termes de minimalité ou maximalité. Les méthodes classiques (équation d’Euler-Lagrange, formulation hamiltonienne et équation de Hamilton-Jacobi) et les méthodes directes (espaces de Sobolev, résultat général et régularité) sont ici explicitées. Le cas vectoriel des méthodes directes est ensuite abordé à l’aide des différentes notions de convexité et d’un résultat d’existence. Les problèmes non convexes du calcul des variations viennent terminer cet article : différentes enveloppes, théorème de relaxation et divers exemples.
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleAuteur(s)
-
Bernard DACOROGNA : Professeur, Section de mathématiques EPFL (École polytechnique fédérale de Lausanne), Suisse
INTRODUCTION
Le calcul des variations est un des sujets classiques des mathématiques. Il a attiré un grand nombre de mathématiciens célèbres. Avant de présenter le cas modèle le plus important, nous allons commencer par une discussion informelle. En mathématiques, en physique, dans les sciences de l'ingénieur ou même en économie ou en écologie, les modèles sont souvent exprimés en termes d'un principe de minimalité ou de maximalité. C'est précisément la question centrale du calcul des variations. Par exemple, en mathématiques, on peut être intéressé à trouver, sous certaines contraintes, une courbe de longueur minimale ou une surface d'aire minimale. En physique, un exemple typique est le principe de moindre action ; d'autres exemples seront donnés dans cet exposé de manière plus détaillée. Par ailleurs, les lois de conservation, qui correspondent mathématiquement à des équations différentielles, sont souvent dérivées à partir d'un principe variationnel. Les solutions du problème variationnel sont alors des solutions d'équations différentielles associées.
L'expertise technique et scientifique de référence
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Mathématiques
(167 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Méthodes directes
English
2. Méthodes classiques
On va se restreindre ici au cas N = n = 1, même si bon nombre de résultats et, notamment, le plus important, se généralisent au cas des dimensions supérieures. Le problème est alors :
où
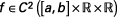
et
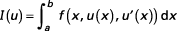
Par la suite, nous dénoterons très souvent les dérivées partielles par des indices.
si f = f (x, u, ξ), alors :
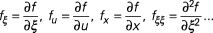
2.1 Équation d'Euler-Lagrange
Le résultat le plus important de cette section est le suivant.
Théorème 1. Soit f ∊ C 2
, f = f (x, u, ξ), et
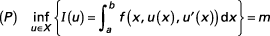
où X = {u ∊ C1 ([a, b]) : u(a) = α, u(b) = β }.
• Première partie. Si (P ) admet un minimiseur :
alors :
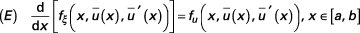
ou, en dérivant :
L'expertise technique et scientifique de référence
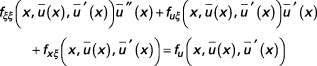
Cet article fait partie de l’offre
Mathématiques
(167 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Méthodes classiques
BIBLIOGRAPHIE
-
(1) - AKHIEZER (N.I.) - The calculus of variations - . Blaisdell, New York (1962).
-
(2) - BLISS (G.) - Lectures on the calculus of variations - . University of Chicago Press, Chicago (1951).
-
(3) - BOLZA (O.) - Lectures on the calculus of variations - . Chelsea Publication, New York (1946).
-
(4) - BUTTAZZO (G.), GIAQUINTA (M.), HILDEBRANDT (S.) - One dimensional variational problems - . Oxford University Press, Oxford (1998).
-
(5) - CARATHÉODORY (C.) - Calculus of variations and partial differential equations of the first order - . Holden Day, San Francisco (1965).
-
(6) - CESARI (L.) - Optimization – Theory and applications - . Springer, New York (1983).
-
...
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Mathématiques
(167 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
