Présentation
Auteur(s)
-
Jean-Marie ESCANÉ : Ingénieur de l’École Supérieure d’Électricité
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleINTRODUCTION
Lensemble des articles sur la théorie des circuits linéaires comprend plusieurs fascicules :
-
[E100] « Définitions. Théorèmes généraux » ;
-
[E102] « Régimes de fonctionnement » ;
-
[E104] « Quadripôles » ;
-
[E106] « Transmittance harmonique et régimes spéciaux » ;
-
[E108] « Systèmes bouclés ».
Un circuit électrique linéaire est soumis à différents régimes de fonctionnement et sa réponse à une excitation dépend à la fois de ses propriétés et de la nature de l’excitation.
Pour être aptes à maîtriser la méthodologie et éviter ainsi des erreurs fatales, il est indispensable d’avoir parfaitement saisi la différence entre les différentes réponses du système : naturelle, forcée, permanente et transitoire. Ces réponses, différentes par nature, s’identifient deux à deux lorsque le système est stable et soumis à une excitation de nature particulière.
Le régime harmonique en est un cas particulier important, mais non le seul, et mérite en raison de ses différentes applications une attention toute particulière.
L'expertise technique et scientifique de référence
VERSIONS
- Version courante de févr. 2011 par André PACAUD
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Électronique
(227 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Différents régimes de fonctionnement. Stabilité2. Régime harmonique
2.1 Représentation des signaux
En régime harmonique, les signaux sont sinusoïdaux, donc représentables par des fonctions sinusoïdales du temps. Considérons alors les signaux
de pulsation ω.
Les grandeurs ϕ1 et ϕ2 sont appelées phases à l’origine de x1(t) et x2(t).
ϕ1 – ϕ2 est appelée différence de phase entre x1 et x2 ou déphasage de x1 sur x2.
-
Représentation vectorielle : x1(t) et x2(t) sont les projections sur l’axe Ox des vecteurs
![]()
et
![]()
tournant autour de O à la vitesse angulaire ω (figure 2). Si l’on ne s’intéresse qu’aux relations entre ces deux grandeurs, on peut faire abstraction de la rotation et ne représenter que la position des vecteurs
![]()
et
![]()
(figure 3).Cette représentation montre que la différence de phase ϕ1 – ϕ2 est équivalente à un retard
![]()
du vecteur
![]()
sur le vecteur
![]()
et
tournant autour de O à la vitesse angulaire ω (figure 
et
(figure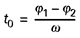 
du vecteur
sur le vecteur
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Électronique
(227 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Régime harmonique
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Électronique
(227 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
