Bibliographie & annexes
Présentation
En anglais
Auteur(s)
-
Mohamed NAJIM : Professeur à l’École nationale supérieure d’électronique et de radioélectricité de Bordeaux (ENSERB)
Lire cet article issu d'une ressource documentaire complète, actualisée et validée par des comités scientifiques.
Lire l’articleINTRODUCTION
L’ingénieur doit souvent considérer le cas courant où l’on souhaite, à partir d’un message brut ou signal observé m (t), contenant un signal utile − signal désiré − et un bruit, à déterminer le meilleur récepteur − optimal − permettant de discriminer le signal du bruit. Par récepteur ou filtre optimal, nous entendons un filtre qui satisfait à un certain critère d’optimalité sous des hypothèses que nous préciserons.
Par filtre, nous entendons une description mathématique des opérations de traitement que subit le signal mélangé au bruit.
Auparavant, nous devons préciser :
1×) que les entrées de ces filtres seront soit des processus aléatoires, soit une combinaison de signaux déterministes et aléatoires. Nous disposerons en général d’un nombre minimal d’informations caractérisant ces entrées ;
2×) que nous ne considérons uniquement les systèmes stationnaires linéaires. Dans les cas où une réalisation matérielle est recherchée, il y aura lieu de considérer la réalisabilité du filtre.
Il sera souvent utile de connaître le système optimal, même s’il n’est pas physiquement réalisable. Sa connaissance permettra de mesurer et d’apprécier les performances des systèmes réalisables mais non optimaux.
Nous traiterons trois types de filtres :
1 - le filtre adapté ;
2 - le filtre de Wiener ;
3 - le filtre de Kalman.
Ces différents filtres correspondent respectivement à une solution dans les cas où :
1×) le signal désiré est de forme connue. Il est mélangé soit à un bruit blanc, soit à un bruit coloré ;
2×) le signal est, à l’instar du bruit, un processus aléatoire. Le filtre développé par Norbert Wiener constitue une solution non récursive, difficile à implanter sur ordinateur ;
3×) le signal et le bruit sont aléatoires. Le filtre de Kalman est une solution récursive du problème du filtrage qui généralise le filtrage de Wiener.
Le développement de ces filtres suppose que l’on dispose d’informations a priori à la fois sur les signaux et sur les bruits. Il s’agit, en particulier, de la connaissance des fonctions ou des matrices d’autocorrélation. Dans le cas où leur connaissance nous fait défaut, on aura comme alternative l’utilisation des filtres adaptatifs. Ces derniers « apprennent » les caractéristiques des signaux au fur et à mesure que ceux-ci se déroulent. On a néanmoins montré récemment qu’une famille de filtres adaptatifs couramment utilisés dans les applications peut, elle aussi, être considérée comme optimale.
L'expertise technique et scientifique de référence
DOI (Digital Object Identifier)
Cet article fait partie de l’offre
Automatique et ingénierie système
(137 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Présentation
Filtre de Kalman
En anglais
2. Filtre de Wiener
2.1 Position du problème
On dispose d’un message m (t ) = s1 (t ) + b1 (t ) où le signal et le bruit sont deux processus aléatoires stationnaires. Il s’agit de trouver le filtre linéaire stationnaire qui donne la meilleure approximation de s1 (t ) notée
. Le signal et le bruit sont deux processus aléatoires stationnaires.
En d’autres termes, il faudra que :
On notera :
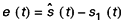
qui constitue l’erreur entre la sortie effective du filtre et la sortie désirée
. Le filtre de Wiener est basé sur la minimisation de l’erreur quadratique moyenne (EQM)
:
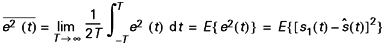
avec :
-
E
![]()
: - opérateur espérance mathématique
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Automatique et ingénierie système
(137 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
Filtre de Wiener
BIBLIOGRAPHIE
-
(1) - WIENER (N.) - Extrapolation, interpolation and smoothing of stationary time series - . MIT Press, 1949. Cambridge, Ma.
-
(2) - LEE (Y.W.) - Statistical theory of communication - . J. Wiley, 1960.
-
(3) - VAN TREES (H.L.) - Detection, estimation and modulation theory - . Tome 1, J. Wiley, 1968.
-
(4) - THOMAS (J.B.) - An introduction to statistical communication theory. - J. Wiley, 1969.
-
(5) - PAPOULIS (A.) - Probability, random variables and stochastic processes - . Mc Graw Hill, 1965.
-
(6) - KALMAN (R.E.), BUCY (R.S.) - New results in linear filtering and prediction theory. - Trans. ASME, Series D, Journal of Basic Eng. vol-38, p. 95-101, 1960.
-
...
L'expertise technique et scientifique de référence
Cet article fait partie de l’offre
Automatique et ingénierie système
(137 articles en ce moment)
Cette offre vous donne accès à :
Une base complète d’articles
Actualisée et enrichie d’articles validés par nos comités scientifiques
Des services
Un ensemble d'outils exclusifs en complément des ressources
Un Parcours Pratique
Opérationnel et didactique, pour garantir l'acquisition des compétences transverses
Doc & Quiz
Des articles interactifs avec des quiz, pour une lecture constructive
